II.I.4 Statistical inference with Ordinary
Least Squares (OLS)
a. Mathematical expectation and variance
of parameters
In
order to be able to say something about the population parameters
(of the real mathematical model), based only on the sample
observations, it is imperative to compute the expectation and the
variance of both estimated parameters.
The
expectation of the estimated
constant term can be
derived as follows
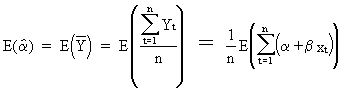
(II.I.4-1)
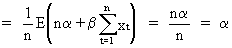
(II.I.4-2)
It
is quite easy to derive the variance of the constant
term as
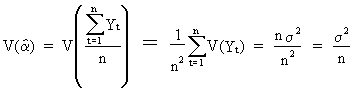
(II.I.4-3)
Now
consider the derivation of the expectation
of the estimated ß parameter
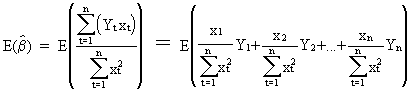
(II.I.4-4)
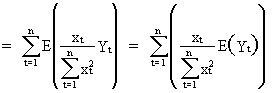
(II.I.4-5)
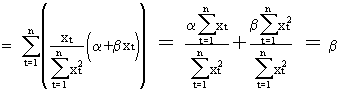
(II.I.4-6)
The
derivation of the variance is quite similar to (II.I.4-4)
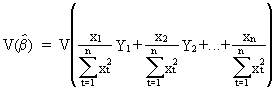
(II.I.4-7)
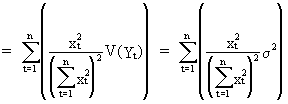
(II.I.4-8)
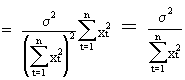
(II.I.4-9)
From
this analysis we conclude that in order to reduce the variance of
the estimated parameters we should ensure that:
 | (a) the
number of sample data should be large because of eq. (II.I.4-3); | |
 | (b)
the
(constant) variance of the endogenous variable should be
relatively small (see eq. (II.I.4-3) and eq. (II.I.4-9)); | |
 | (c) the
range of the exogenous variable should be large because of eq.
(II.I.4-9). | |
Remark that
(a) and (c) is not only true in simple regression but also in all other
econometric regressions (time series and cross-sectional data),
multivariate statistic techniques, statistic time series analyses,
random experiments, and even in controlled experiments (this only
applies to (c) ).
Furthermore, it can be
concluded from eq. (II.I.4-2)and eq. (II.I.4-6)that OLS for simple
regression yields unbiased
estimates for both parameters.
b. Confidence intervals for the parameters
In order to find
the t statistic we first derive the Z transformation of the
estimated value of ß
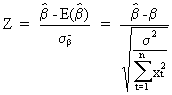
(II.I.4-10)
where the
unobservable s
is replaced by the sample variance since
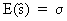
(II.I.4-11)
so that by
definition
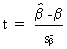
(II.I.4-12)
Furthermore, the
95% confidence interval for any ß parameter is given by
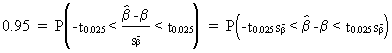
(II.I.4-13)
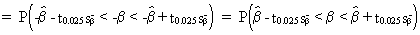
(II.I.4-14)
where
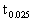
represents the
limit value of ß according to the students t-distribution (for the
5% significance level).
The confidence
interval for a
can be found in just the same way (cfr. (II.I.4-10) to (II.I.4-14)).
c. Forecasting errors
If the mean
forecast is considered, a suitable confidence interval should be
derived.
First we
note
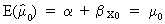
(II.I.4-15)
(we say: the mean estimator (II.I.4-15) is unbiased).
Additionally, the
expression for the variance
of the mean estimator is found as
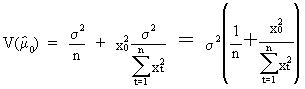
(II.I.4-16)
Example of interpolation confidence interval
It is obvious from
(II.I.4-16) that the forecast performance depends on: the variance
of the endogenous variable, the sample size, the range of the
exogenous variable, and x0; the distance between the
forecast origin and the mean of the exogenous variable.
If however, an
individual estimation of Y at origin t = o (o = origin) has to be
performed, the variance should be added to (II.I.4-16)
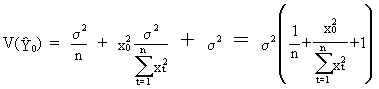
(II.I.4-17)
| 
