V.I.1.a Basic Definitions and
Theorems about ARIMA models
First
we define some important concepts. A stochastic process (c.q. probabilistic process) is defined by a
T-dimensional distribution function.
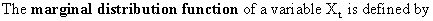
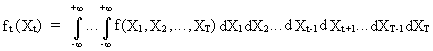
(V.I.1-1)
Before
analyzing the structure of a time series model one must make sure
that the time series are stationary with respect to the variance and
with respect to the mean. First, we will assume statistical
stationarity of all time series (later on, this restriction will be
relaxed).
Statistical
stationarity
of a time series implies that the marginal probability distribution
is time-independent which means that:
 |
the
expected values and variances are constant | |
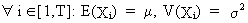
(V.I.1-2)
where
T is the number of observations in the time series;
 |
the
autocovariances (and autocorrelations) must be constant | |
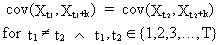
(V.I.1-3)
where
k is an integer time-lag;
 |
the
variable has a joint normal distribution f(X1, X2,
..., XT) with marginal normal distribution in each
dimension | |
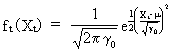
(V.I.1-4)
If
only this last condition is not met, we denote this by weak
stationarity.
Now
it is possible to define white noise as a stochastic process
(which is statistically stationary) defined by a marginal
distribution function (V.I.1-1), where all Xt are
independent variables (with zero covariances), with a joint normal
distribution f(X1, X2, ..., XT),
and with
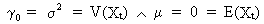
(V.I.1-5)
It
is obvious from this definition that for any white noise process the
probability function can be written as
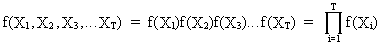
(V.I.1-6)
Define
the autocovariance as
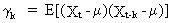
(V.I.1-7)
or
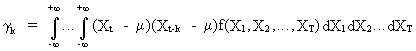
(V.I.1-8)
whereas
the autocorrelation is
defined as
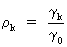
(V.I.1-9)
In
practice however, we only have the sample observations at our
disposal. Therefore we use the sample autocorrelations
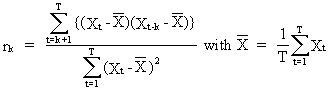
(V.I.1-10)
for
any integer k.
Remark
that the autocovariance
matrix and autocorrelation
matrix associated
with a stochastic stationary process
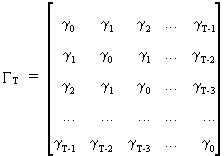
(V.I.1-11)
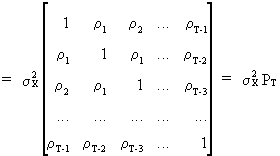
(V.I.1-12)
is
always positive definite, which can be easily shown since a linear
combination of the stochastic variable
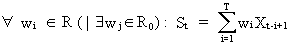
(V.I.1-13)
has
a variance of
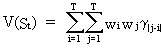
(V.I.1-14)
which
is always positive.
This
implies for instance for T=3 that
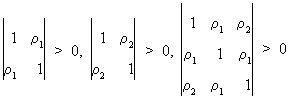
(V.I.1-15)
or
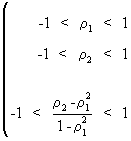
(V.I.1-16)
Bartlett
proved that the variance of
autocorrelation of a stationary normal stochastic process can be
formulated as
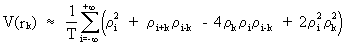
(V.I.1-17)
This
expression can be shown to be reduced to
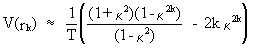
(V.I.1-18)
if
the autocorrelation coefficients decrease exponentially like
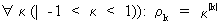
(V.I.1-19)
Since
the autocorrelations for i > q (a natural number) are equal to
zero, expression (V.I.1-17) can be shown to be reformulated as
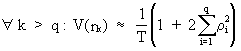
(V.I.1-20)
which
is the so called large-lag
variance. Now it is possible to vary q from 1 to any desired
integer number of autocorrelations, replace the theoretical
correlations by their sample estimates, and compute the square root
of (V.I.1-20) to find the standard deviation of the sample
autocorrelation.
Note
that the standard deviation
of one autocorrelation coefficient is almost always approximated by
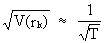
(V.I.1-21)
The
covariances between
autocorrelation coefficients have also been deduced by Bartlett
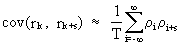
(V.I.1-22)
which
is a good indicator for dependencies between autocorrelations.
Remind therefore that inter-correlated autocorrelations can
seriously distort the
picture of the autocorrelation
function (ACF c.q. autocorrelations as a function of a
time-lag).
It
is however possible to remove the intervening correlations between Xt
and Xt-k by defining a partial autocorrelation
function (PACF)
The
partial autocorrelation coefficients are defined as the last
coefficient of a partial autoregression equation of order k
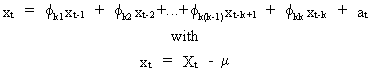
(V.I.1-23)
It
is obvious that there exists a relationship
between the PACF and the ACF since (V.I.1-23) can be rewritten
as
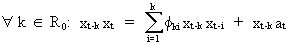
(V.I.1-24)
or
(on taking expectations and dividing by the variance)
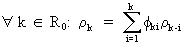
(V.I.1-25)
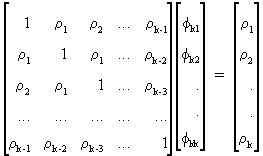
Sometimes
(V.I.1-25) is written in matrix formulation according to the Yule-Walker relations
(V.I.1-26)
or
simply
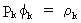
(V.I.1-27)
Solving
(V.I.1-27) according to Cramer's Rule yields

(V.I.1-28)
Note
that the determinant of the numerator contains the same elements as
the determinant of the denominator, except for the last column that
has been replaced.
A
practical numerical
estimation algorithm for the PACF is given by Durbin
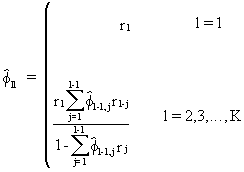
(V.I.1-29)
with
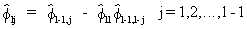
(V.I.1-30)
The
standard error of a partial
autocorrelation coefficient for k > p (where p is the order
of the autoregressive data generating process; see later) is given
by
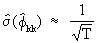
(V.I.1-31)
Finally,
we define the following polynomial
lag-processes
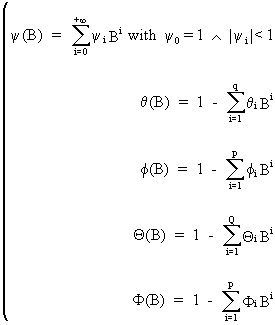
(V.I.1-32)
where
B is the backshift operator (c.q. BiYt
= Yt-i) and where
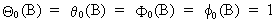
(V.I.1-33)
These
polynomial expressions are used to define linear
filters. By definition a linear filter
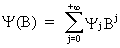
(V.I.1-34)
generates
a stochastic process
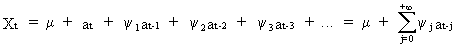
(V.I.1-35)
where
at is a white noise variable.

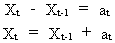
(V.I.1-36)
for
which the following is obvious
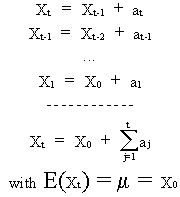
(V.I.1-37)
We
call eq. (V.I.1-36) the random-walk model: a model that
describes time series that are fluctuating around X0 in
the short and in the long run (since at is white noise).
It
is interesting to note that a random-walk is normally distributed. This can be proved by using the definition of
white noise and computing the moment generating function of the
random-walk
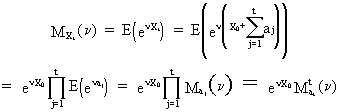
(V.I.1-38)

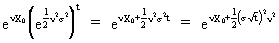
(V.I.1-39)
from
which we deduce
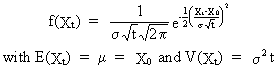
(V.I.1-40)
(Q.E.D.).
A
deterministic trend is
generated by a random-walk model with an added constant
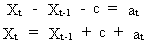
(V.I.1-41)
The
trend can be illustrated by re-expressing (V.I.1-41) as
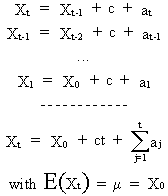
(V.I.1-42)
where
ct is a linear deterministic trend (as a function of time).
The
linear filter (V.I.1-35)
is normally distributed
with
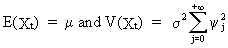
(V.I.1-43)
due
to the additivity property of eq. (I.III-33), (I.III-34), and
(I.III-35) applied to at.
Now
the autocorrelation of a linear filter can be quite easily computed as
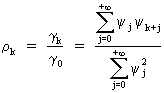
(V.I.1-44)
since
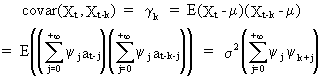
(V.I.1-45)
and
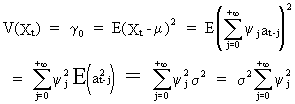
(V.I.1-46)
Now
it is quite evident that, if the linear filter (V.I.1-35) generates
the variable Xt,
then Xt
is a stationary stochastic
process ((V.I.1-1) - (V.I.1-3))
defined by a normal distribution (V.I.1-4)
(and therefore strongly stationary), and a autocovariance function
(V.I.1-45) which is only dependent on the time-lag k.
The
set of equations resulting from a linear filter (V.I.1-35)
with ACF (V.I.1-44) are
sometimes called stochastic
difference equations. These stochastic difference equations can
be used in practice to forecast (economic) time series. The forecasting
function is given by
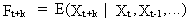
(V.I.1-47)
On
using (V.I.1-35), the
density of the forecasting function (V.I.1-47) is
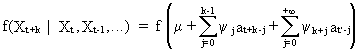
(V.I.1-48)
where
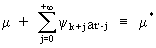
(V.I.1-49)
is
known, and therefore equal to a constant term. Therefore it is
obvious that
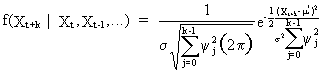
(V.I.1-50)
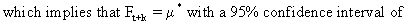
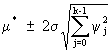
(V.I.1-51)
The
concepts defined and described above are all time-related. This
implies for instance that autocorrelations are defined as a function
of time. Historically, this time-domain
viewpoint is preceded by the frequency-domain
viewpoint where it is assumed that time series consist of sine and
cosine waves at different frequencies.
In
practice there are both advantages and disadvantages to both
viewpoints. Nevertheless, both should be seen as
complementary to each other.
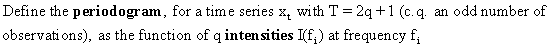
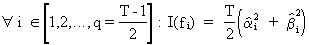
(V.I.1-52)
for
the Fourier
series model
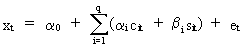
(V.I.1-53)
In
(V.I.1-53) we define
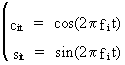
(V.I.1-54)
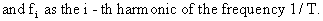
The
least squares estimates
of the parameters in (V.I.1-52) are computed by
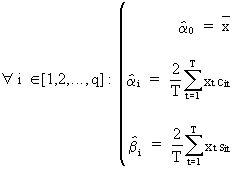
(V.I.1-55)
In
case of a time series with an even number of observations T = 2 q
the same definitions are applicable except for
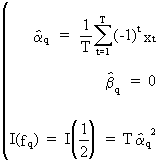
(V.I.1-56)
It
can furthermore be shown that
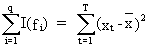
(V.I.1-57)

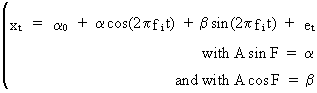
(V.I.1-58)
such
that
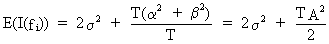
(V.I.1-59)
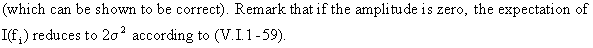
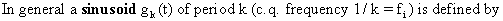
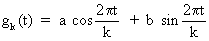
(V.I.1-60)
Obviously
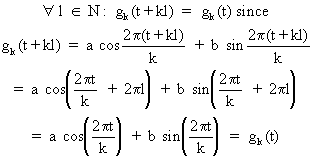
(V.I.1-61)
It
is also possible to show that
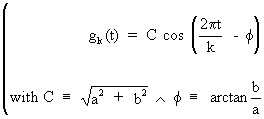
(V.I.1-62)
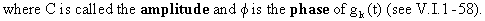
If
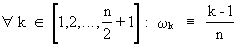
(V.I.1-63)
then
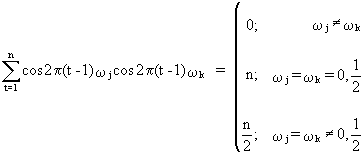
(V.I.1-64)
and
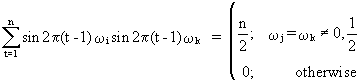
(V.I.1-65)
and
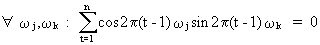
(V.I.1-66)
and
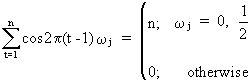
(V.I.1-67)
and
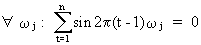
(V.I.1-68)
which
state the orthogonality
properties of sinusoids and which can be proved. Remark that
(V.I.1-67) is a special case of (V.I.1-64) and (V.I.1-68) is a
special case of (V.I.1-66). Particularly eq. (V.I.1-66) is
interesting for our discussion in regard to (V.I.1-60) and (V.I.1-53),
since it states that sinusoids are independent.
If
(V.I.1-52) is
redefined as
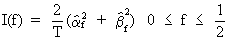
(V.I.1-69)
then
I(f) is called the sample
spectrum.
The
sample spectrum is in fact a Fourier cosine transformation of the
autocovariance function estimate. Denote the covariance-estimate of
(V.I.1-7)by the sample-covariance (c.q. the numerator of
(V.I.1-10)), the complex number
i, and the frequency by f, then
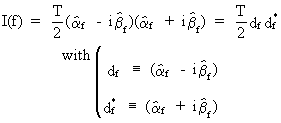
(V.I.1-70)
On
using (V.I.1-55)and
(V.I.1-70) it follows that
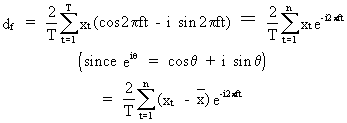
(V.I.1-71)
which
can be substituted into (V.I.1-70) yielding
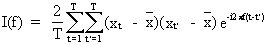
(V.I.1-72)
Now
from (V.I.1-10) it follows
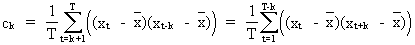
(V.I.1-73)
and
if (t - t') is substituted by k then (V.I.1-72) becomes
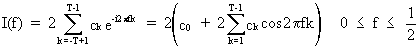
(V.I.1-74)
which
proves the link between the sample spectrum and the estimated
autocovariance function.
On
taking expectations of the spectrum we obtain
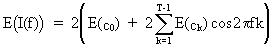
(V.I.1-75)
for
which it can be shown that
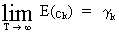
(V.I.1-76)
On
combining (V.I.1-75) and (V.I1.1-76) and on defining the power
spectrum as p(f) we find
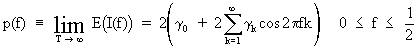
(V.I.1-77)
It
is quite obvious that
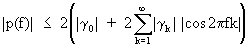
(V.I.1-78)
so
that it follows that the power spectrum converges if the covariance
decreases rather quickly. The power spectrum is a Fourier cosine
transformation of the (population) autocovariance function. This
implies that for any theoretical autocovariance function (cfr. the
following sections) a respective theoretical power spectrum can be
formulated.
Of
course the power spectrum can be reformulated with respect to
autocorrelations in stead of autocovariances
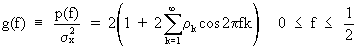
(V.I.1-79)
which
is the so-called spectral
density function.
Since
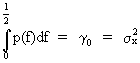
(V.I.1-80)
it
follows that
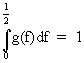
(V.I.1-81)
and
since g(f) > 0 the properties of g(f) are quite similar to those
of a frequency distribution function.
Since
it can be shown that the sample spectrum fluctuates wildly around
the theoretical power spectrum a modified (c.q. smoothed) estimate
of the power spectrum is suggested as
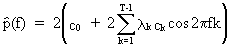
(V.I.1-82)

| 
