Free Statistics Calculator
Our calculator allows you to compute Simple Linear Regression statistics for any pair of data series.
Data
Example Data Set & Computation (°)
Download
MS Excel Sheet.
Output
| Observations |
Computation |
| # |
y |
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
| 1 |
3 |
1 |
-5 |
-2 |
25 |
4 |
10 |
0.0 |
0.00 |
0.00 |
| 2 |
5 |
2 |
-3 |
-1 |
9 |
1 |
3 |
-0.5 |
0.25 |
0.50 |
| 3 |
7 |
3 |
-1 |
0 |
1 |
0 |
0 |
-1.0 |
1.00 |
1.00 |
| 4 |
14 |
4 |
6 |
1 |
36 |
1 |
6 |
3.5 |
12.25 |
3.50 |
| 5 |
11 |
5 |
3 |
2 |
9 |
4 |
6 |
-2.0 |
4.00 |
2.00 |
| Sum |
40 |
15 |
0 |
0 |
80 |
10 |
25 |
0.0 |
17.50 |
7.00 |
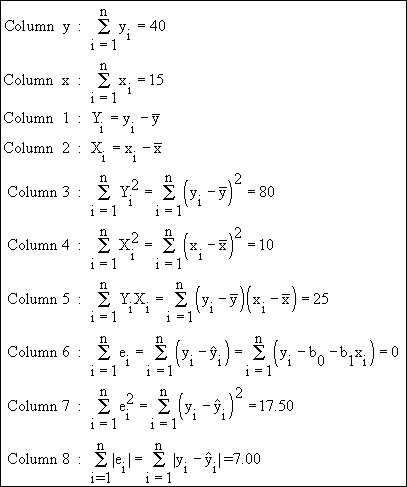
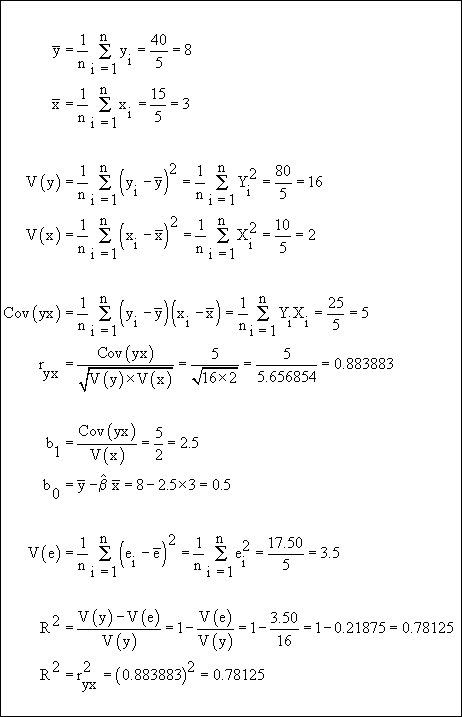
Computations 2
+----------------+
¦ COEFFICIENTS 1 ¦
+----------------+
Variable Coefficient Stand.Err. t-Ratio Probability
INTERCEPT .500000
St1X5 2.500000 .763763 3.273267 .023331 +----------------+
¦ COEFFICIENTS 2 ¦
+----------------+
Variable Elasticity Stand.Err. t-Ratio Probability
St1X5 .937500 .286411 -.218218 .579370 +----------------+
¦ COEFFICIENTS 3 ¦
+----------------+
Variable Coefficient Stand.Coef. Elasticity Rel.Contr.
INTERCEPT .500000
St1X5 2.500000 .883883 .937500 1.000000 +----------------------------------+
¦ ANALYSIS OF VARIANCE 1 : GENERAL ¦
+----------------------------------+
ANOVA df Sum of Squares Mean Square
Mean 1 320.000000
Regression 1 62.500000 62.500000
Residual 3 17.500000 5.833330
Total 5 400.000000 80.000000
F-Test Statistic Value : 10.714300
Degrees of Freedom 1 : 1
Degrees of Freedom 2 : 3
Probability : .046662+------------------------------------+
¦ ANALYSIS OF VARIANCE 2 : FROM MEAN ¦
+------------------------------------+
ANOVA df Sum of Squares Mean Square
Regression 1 62.500000 62.500000
Residual 3 17.500000 5.833330
Total 4 80.000000 20.000000
F-Test Statistic Value : 10.714300
Degrees of Freedom 1 : 1
Degrees of Freedom 2 : 3
Probability : .046662+------------------------------------+
¦ ANALYSIS OF VARIANCE 3 : FROM ZERO ¦
+------------------------------------+
ANOVA df Sum of Squares Mean Square
Regression 2 382.500000 191.250000
Residual 3 17.500000 5.833330
Total 5 400.000000 80.000000
F-Test Statistic Value : 32.785733
Degrees of Freedom 1 : 2
Degrees of Freedom 2 : 3
Probability : .009151+-----------------+
¦ AUTOCORRELATION ¦
+-----------------+
Durbin-Watson Statistic : 2.914286
Von Neumann Ratio : 3.642857
rho - Least Squares : -.740741
rho - Maximum Likelihood : -.571429
rho - Serial Correlation : -.714286
rho - Goldberger : -.650600
Number of Observations : 5 +--------------------+
¦ MEAN AND VARIANCES ¦
+--------------------+
Variable y Observed Mean : 8.000000
Unbiased Variance : 20.000000
St. Dev. : 4.472136
Biased Variance : 16.000000
St. Dev. : 4.000000
Variable y Calculated Mean : 8.000000
Unbiased Variance : 15.625000
St. Dev. : 3.952847
Biased Variance : 12.500000
St. Dev. : 3.535534
Error Mean : .000000
Unbiased Variance : 4.375000
St. Dev. : 2.091650
Biased Variance : 3.500000
St. Dev. : 1.870829
Number of Observations : 5+--------------+
¦ CORRELATIONS ¦
+--------------+
Correlation Y Observed vs. Y Calculated : .883883
Y Observed vs. Errors : .467707
Y Calculated vs. Errors : .000000
Multiple Correlation Coefficient : .883883
Coefficient of Determination Non Adjusted : .781250
Adjust.1 : .708333
Adjust.2 : .718274
Number of Observations : 5
Number of Explanatory Variables : 2+-----------------+
¦ MODEL SELECTION ¦
+-----------------+
Akaike Final Prediction Error FPE : 8.166667
Information Criterion AIC : 7.789393
Information Criterion ln AIC : 2.052763
Amemiya Prediction Criterion APC : 8.166667
Craven-Wahba Generalized Cross Validation GCV : 9.722222
Hannan-Quinn Criterion HQC : 5.121621
Rice Criterion RC : 17.500000
Schwartz Criterion SC : 6.662789
Criterion ln SC : 1.896538
Shibata Criterion SHC : 6.300000
Error Biased Variance : 3.500000
Log Likelihood Function : -10.226600
Multiple Correlation Coefficient : .883883
Coefficient of Determination Non Adjusted : .781250
Adjust.1 : .708333
Adjust.2 : .718274
Number of Observations : 5
Number of Explanatory Variables : 2+-------------------+
¦ MODEL PERFORMANCE ¦
+-------------------+
Sum Squared Error SSE : 17.500000
Mean Squared Error MSE : 3.500000
Root Mean Squared Error RMS : 1.870829
Error Biased Variance : 3.500000
Variance of Estimate : 5.833333
Standard Error of Estimate : 2.415229
Log Likelihood Function : -10.226600
Multiple Correlation Coefficient : .883883
Coefficient of Determination Non Adjusted : .781250
Adjust.1 : .708333
Adjust.2 : .718274
z-Transform of Correlation Coefficient : 1.393248
F-Test Statistic : 10.714286
Degrees of Freedom d1 : 1
d2 : 3
Probability : .046662
Number of Observations : 5
Number of Explanatory Variables : 2+------------------+
¦ ERROR STATISTICS ¦
+------------------+
Error Mean ME : .000000
Squared Mean MES : .000000
Variance Biased VARE : 3.500000
St. Dev. Biased : 1.870829
Variance Unbiased : 4.375000
St. Dev. Unbiased : 2.091650
Relative Error Standard Deviation : .233854
Mean Squared Error MSE : 3.500000
Root Mean Squared Error RMS : 1.870829
Relative Root Mean Squared Error RRMS : .535069
Mean Percentage Error MPE : 2.519320
Mean Absolute Error MAE : 1.400000
Mean Absolute Percentage Error MAPE1 : .134935
MAPE2 : .136190
Variation Coefficient VC1 : 23.385359
VC2 : **************
Number of Observations : 5+----------------------+
¦ DECOMPOSITION OF MSE ¦
+----------------------+
Theil's Inequality Coefficient TH : .105752
IC : .209165
IC2 : .043750
Mean Squared Error MSE : 3.500000
Proportion due to Bias UM : .000000
Variance US : .061637
Covariance UC : .938363
Proportion due to Bias UM : .000000
Regression UR : .000000
Disturbance UD : 1.000000
Number of Observations : 5
Output - Graphical
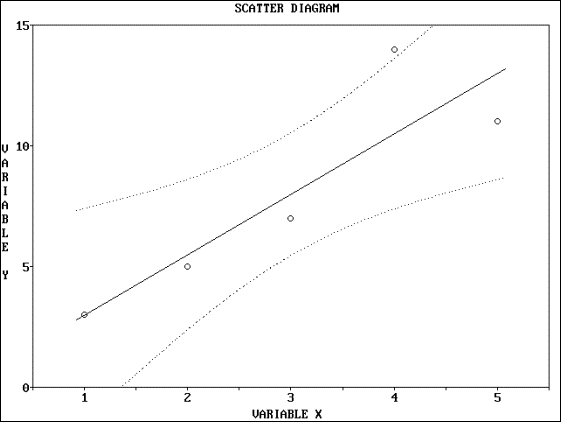
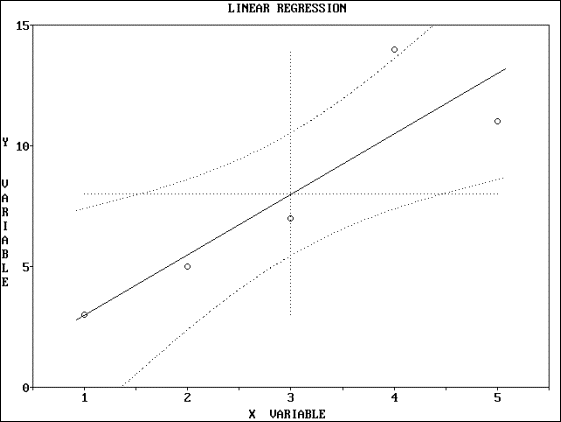
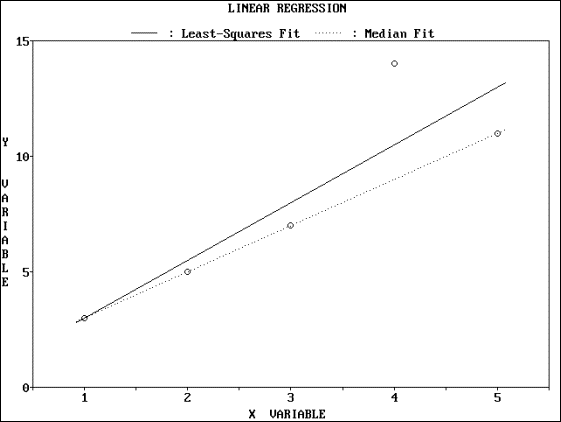
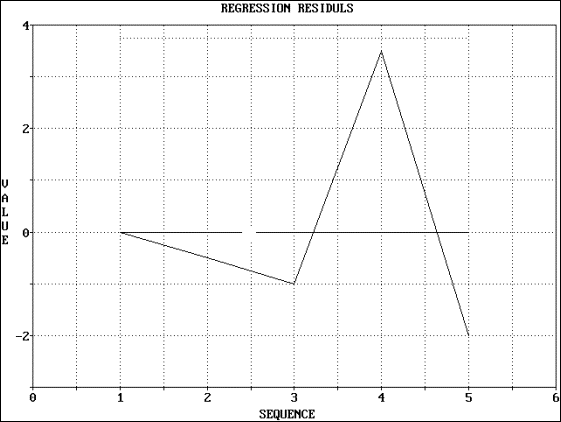
References
Barten, A.
Note on Unbiased Estimation of the Squared Multiple Correlation Coefficient
Statistica Neerlandica, vol. 16, no. 2, 1962, pp. 151-163.
Durbin, J. and Watson, G.
Testing for Serial Correlation in Least-Squares Regression I
Biometrika, vol. 37, 1950, pp. 409-428.
Durbin, J. and Watson, G.
Testing for Serial Correlation in Least-Squares Regression II
Biometrika, vol. 38, 1951, pp. 159-178.
Forecasts and Realizations
Central Planning Bureau Monograph no.10
Staatsdrukkerij, ´s-Gravenhage, 1965.
Goldberger, A.
Econometric Theory
John Wiley, London, 1964, pp. 197-198.
Jarque, C.M. and Bera, A.K.
A Test for Normality of Observations and Regression Residuals
International Statistical Review, vol. 55, 1987, pp. 163-172.
Judge, G. et al.
The Theory and Practice of Econometrics
John Wiley, New York, 2nd Ed., 1985, p. 242.
Malinvaud, E.
Statistical Methods of Econometrics
Studies in Mathematical and Managerial Economics VI
North-Holland, Amsterdam, 2nd Ed., 1970, p.520.
Press, W.H. et al.
Numerical Recipes in Pascal - The Art of Scientific Computing
Cambridge University Press, Cambridge, 1989, pp. 543-545.
Ramanathan, R.
Introductory Econometrics with Applications
Harcourt Brace Jovanovich, San Diego, 2nd Ed., 1992, p. 167.
Theil, H.
Econometric Forecasts and Policy
Contributions to Economic Analysis XV
North-Holland, Amsterdam, 2nd Ed., 1961, pp. 26-43.
| 
