III.VI.1
Finite distributed lags
We
define finite distributed lags by the following underlying model
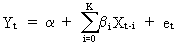
(III.VI.1-1)
where
K is the (finite) number of lags to be considered. Apparently,
estimation of (III.VI.1-1) for K smaller than T is easily obtained
by the OLS estimator which is, under OLS assumptions, BLUE.
Remark
however that in practice estimation of (III.VI.1-1) might become
difficult due to the possibility of multicollinearity (due to high
autocorrelation in X).
Also
note that in this model K is assumed to be known. If this parameter
is not specified correctly the existence of an Unobserved Variables
Bias is quite
realistic. Therefore a selection criterion is often used to specify
the lag length. One of the most popular criteria is the Akaike Information Criterion (AIC)
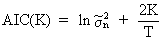
(III.VI.1-2)
where
sigma is the maximum likelihood estimator for the variance (cfr.
(II.II.2-7)). The AIC criterion must be
minimized to find the optimal model structure.
Remark
however that all selection criteria found in the econometrics
literature should be used with great care! According to Judge et al.
: "Although there is a
certain intuitive appeal and logic to many of the ad hoc, informal
model selection rules that have been suggested, we should not forget
(1) their heuristic
base, (2) the fact
that their sampling properties are virtually unknown, and
(3) that their practical
utility is mainly demonstrated by numerical examples."
(Judge et al. 1985, p. 888).
When
it is assumed that the b
coefficients are polynomially distributed according to a finite time
lag, we call these Almon lags.
Finite polynomially distributed lags of order Q can be written as
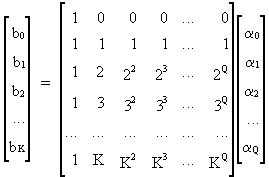
(III.VI.1-3)
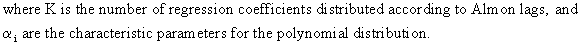
Obviously,
a shorter description of (III.VI.1-3) is
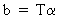
(III.VI.1-4)


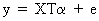
(III.VI.1-5)
it
follows that
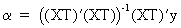
(III.VI.1-6)
or
(in terms of the original parameters)
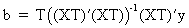
(III.VI.1-7)
which
is in fact a kind of RLS estimator for the polynomially distributed b
parameter vector.
Under
OLS assumptions it can be shown that
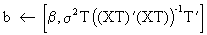
(III.VI.1-8)
In
practice it follows from the above that estimation of Almon lags is
quite simple if K and Q are known beforehand. This however is not
always the case, moreover there exist a lot of difficulties in
identifying K and Q. As mentioned earlier, the ad hoc selection
criteria should be used with great care.
Sometimes
it is assumed that the regression parameters follow a polynomial
spline lag. Formally this is
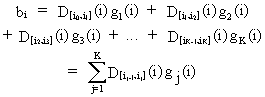
(III.VI.1-9)
where
iK is the true lag length, and
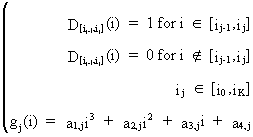
(III.VI.1-10)
In
order to obtain a smooth distribution it is necessary to impose the
following structure on the cubic polynomials
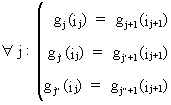
(III.VI.1-11)
Now
the same procedure as with the Almon lags is used to derive the
polynomial spline lag estimator
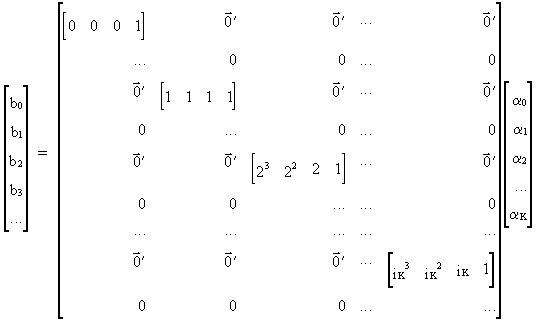
(III.VI.1-12)
with
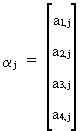
(III.VI.1-13)
Compactly
this can be written like (III.VI.1-4)
and the appropriate RLS estimator is analogous to the derivation of
the Almon lag estimator.
Last
but not least define the harmonic
distributed lag as
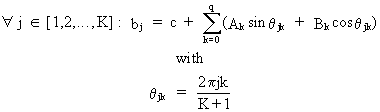
(III.VI.1-14)

Eq.
(III.VI.1-14) becomes (III.VI.1-7)
in short notation and
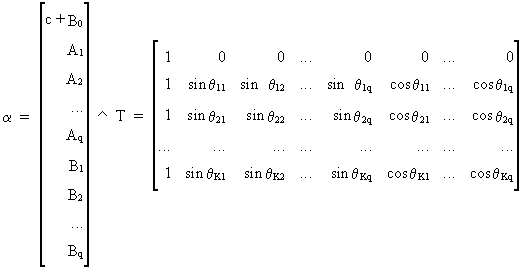
(III.VI.1-15)
Obviously,
estimation of these harmonic distributed lags is analogous to the
estimation of Almon lags. | 
